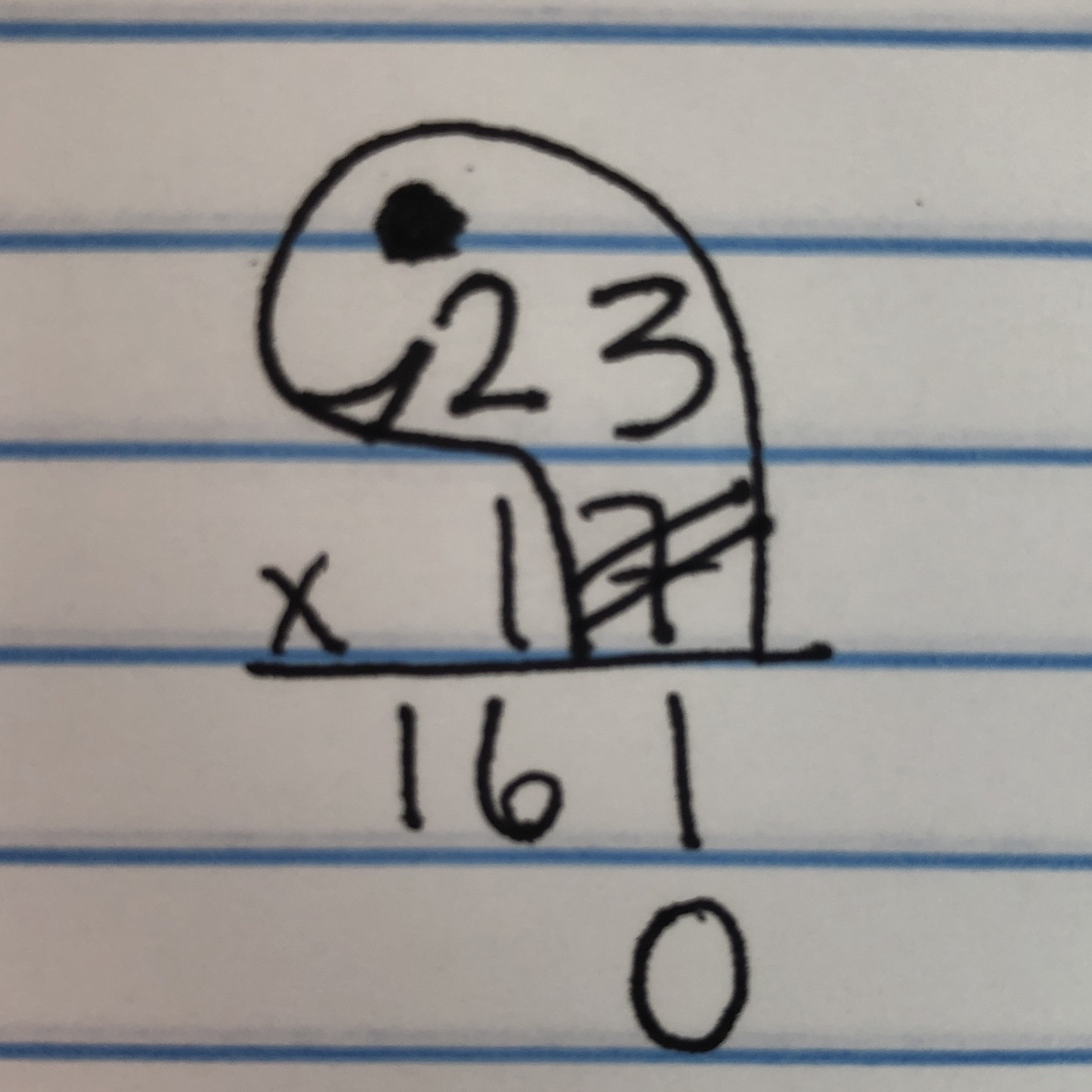
Chances are that unless you were an elementary student or teacher in the last few years, you learned to solve multi-digit multiplication through the use of a procedure known as the standard algorithm (see example below).

The great thing about the standard algorithm is that it’s fast and it takes up less room than some other methods. The downside? If you’re anything like me (and many adults and students I’ve worked with over the last few years) you learned this procedure without questioning why it works and were only concerned with getting the right answer.
Believe it or not, some of us elementary teachers honestly don’t know how the standard algorithm for multi-digit multiplication works either (which is a problem for another post). Even if you were curious as to how this procedure worked, you might have been told something like, “It just does” because your teacher or another well-meaning adult couldn’t explain it themselves and felt anxious or intimidated at the thought that they were unsure of this seemingly mysterious series of steps to arrive at a correct solution.
When teachers (and other well-meaning adults) can’t explain something in a way that students can understand, sometimes they resort to cute tricks, gimmicks, and shortcuts. Recently, I was introduced to one of these gimmicks for remembering to place a zero in the correct spot for a two-digit by two-digit multiplication problem while working with a student I was tutoring. I asked this student to solve for 23×17 however she knew how, and I wrote it down horizontally as to discourage any one method over another. She rewrote the expression and solved it using the standard algorithm and arrived at a correct solution with limited effort.
After congratulating her for solving correctly, I asked if she could help me understand what she did. She walked me through each step of the procedure, telling me exactly what she did in perfect sequence, but couldn’t tell me why she did it that way. Of particular interest to me, she couldn’t explain why she “carried the two” or wrote a zero on the line underneath 161 before “multiplying by one.”
When I asked her why she thought she wrote a zero, she thought hard and said she wasn’t sure, but she knew it was the right thing to do because her teacher told her, “The turtle lays an egg.”
A what?!
Bewildered, I couldn’t help but laugh while letting her know I genuinely wanted to see how her teacher showed her to remember the steps for multi-digit multiplication since it involved turtles. Smiling, she walked me through the procedure (see example below).

Smiling, I asked her what turtles laying eggs had to do with multiplication. She joined in the laugher and shrugged as she told me she didn’t know that either. Through more laughter, I let her know that it wasn’t her fault she didn’t know what she was doing, and that we’d figure it out together (which we did next).
Here’s two takeaways I learned from my encounter with this incredibly bright, young student:
- Students are paying attention to our instruction! She was able to teach me the exact procedure she learned in class.
- Cute tricks and gimmicks require zero reasoning and do not lead to sense-making. Tricks and gimmicks have no place in mathematics.
By the way, this student’s mother messaged me after our most recent tutoring session together and I was overjoyed at what she sent.


